快速傅里叶变换--用于变调

快速傅里叶变换–用于变调

曹逸君张思雨

PS:用于交线性代数报告，线代的应用。

对傅里叶变换的理解

看了视频课、各种博文。对傅里叶变换(FFT)理解如下：
傅里叶变换有各种变体，
1. 非周期性连续信号傅立叶变换（Fourier Transform）
2. 周期性连续信号傅立叶级数(Fourier Series)
3. 非周期性离散信号离散时域傅立叶变换（Discrete Time Fourier Transform）
4. 周期性离散信号离散傅立叶变换(Discrete Fourier Transform)
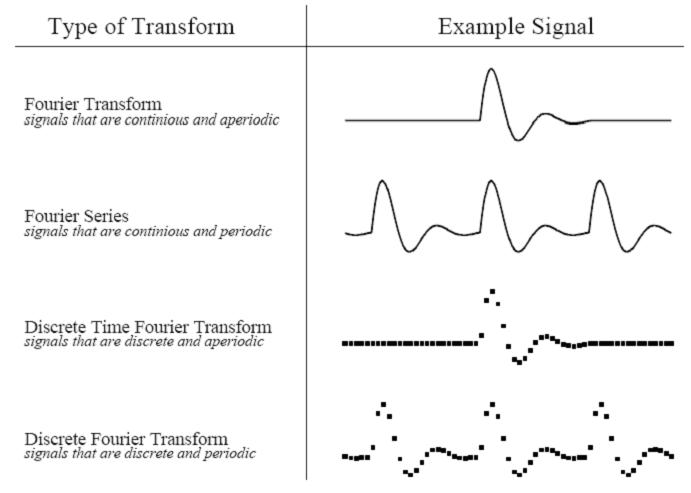
图示各变体

实际信号处理中，都是用的离散傅立叶变换(DFT)，因为计算机能处理得只能是离散得值。

而快速傅里叶变换(FFT)则是将傅里叶变换的时间复杂度降至 $n*log(n)$ 的改进算法。

傅里叶变换总的来说是将函数从基于时域和频域得相互转换得变换。
或者说成将任意(连续周期，数学上得要求，实际操作上可以对任意数据进行。)函数分解为多个正余弦函数。

傅里叶矩阵与傅里叶变换

复矩阵

复向量的模复向量 $z\in { C }^{ n }$ 其模 $|z|={ z }^{ H }z={ \bar{z} }^{ T }z$
zH表示对向量z的转置并共轭，H代表埃尔米特Hermite
复向量的内积： ${ x }^{ H }y$
埃尔米特矩阵： ${ A }^{ H }=A$ 当 $A$ 是实矩阵时，即为对称矩阵。
对称矩阵和埃尔米特矩阵的特征值是实数，特征向量相互垂直。
复矩阵正交称为酉矩阵(unitary)，有 ${ Q }^{ H }Q=I$ 即 ${ Q }^{ -1 }=Q^{ H }$

傅里叶矩阵

F n = ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ 111111 1 w w 2 w 3 ⋮ w (n - 1) 1 w 2 w 4 w 6 ⋮ w 2 (n - 1) 1 w 3 w 6 w 9 ⋮ w 3 (n - 1) 1 \dots \dots \dots ⋱ w n (n - 1) 1 w (n - 1) w 2 (n - 1) w 3 (n - 1) w n (n - 1) w (n - 1) 2 ⎞ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟

${ F }_{ n }=\begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & w & { w }^{ 2 } & { w }^{ 3 } & \cdots & { w }^{ (n-1) } \\ 1 & { w }^{ 2 } & { w }^{ 4 } & { w }^{ 6 } & \cdots & { w }^{ 2(n-1) } \\ 1 & { w }^{ 3 } & { w }^{ 6 } & { w }^{ 9 } & \cdots & { w }^{ 3(n-1) } \\ 1 & \vdots & \vdots & \vdots & \ddots & { w }^{ n(n-1) } \\ 1 & { w }^{ (n-1) } & { w }^{ 2(n-1) } & { w }^{ 3(n-1) } & { w }^{ n(n-1) } & { w }^{ { (n-1) }^{ 2 } } \end{pmatrix}$ 傅里叶矩阵是个特殊的酉矩阵。其中

w $w$ 满足

wn=1 $w^n=1$ 。用复指数表示为

w=ei2πn $w=e^{ \frac { i2\pi }{ n } }$ 。PS:上帝公式

eiπ=−1 $e^{i\pi}=-1$ 。

将原始数据向量左乘傅里叶矩阵就完成了傅里叶变换。
左乘傅里叶矩阵的逆矩阵 $A^{-1}=A^{H}$ 就是傅里叶逆变换。

快速傅里叶变换(FFT)

由于傅里叶矩阵各列正交。又呈实矩阵那样得对称性。故可以将其分解。

(F 64) = (I I D - D) (F 32 0 0 F 32) (P)

$\begin{pmatrix} { F }_{ 64 } \end{pmatrix}=\begin{pmatrix} I & D \\ I & -D \end{pmatrix}\begin{pmatrix} { F }_{ 32 } & 0 \\ 0 & { F }_{ 32 } \end{pmatrix}\begin{pmatrix} P \end{pmatrix}$

$P$ 是奇偶置换矩阵。 $D=\begin{pmatrix} 1 & & & & \\ & w & & & \\ & & { w }^{ 2 } & & \\ & & & \ddots & \\ & & & & { w }^{ 31 } \end{pmatrix}$ 。并且 ${w}_{32}={{w}_{64}}^{2}$ 。

如上分解可以迭代下去到一阶傅里叶矩阵。而计算量也由 $n^2$ 降为 $\frac{1}{2}n log(n)$ 。